Grind For Yellow - Colorful Graph

Solved: ✅
Difficulty: ★★★☆☆☆
Uniqueness: ★★★☆☆☆

Problem Statement

As always, you can find the problem link here for those who want to try solving it on their own. For those who need a translation of the problem statement, here it is:

There is a simple graph with $N$ vertices and $M$ undirected edges. Initially, all nodes are colored with $1$-st color. You are given $Q$ operations, each specified as $x\ y$, which colors the $x$-th node and its neighbours with the $y$-th color.

For each operation, print the color of the node before the operation.

Intuition

Initially, brute forcing the problem seems like a straightforward approach. For each operation $x\ y$, this method will take $O(deg(x))$. However, in the worst-case scenario, repeated operations on high-degree nodes could lead to a time complexity of $O(V)$ per operation.

We can consider two strategies to address this question:

1. Is there a method to handle all nodes more efficiently?
2. If the degrees of $x$ are mostly small, the $O(deg(x))$ complexity isn’t problematic. Can we handle nodes with large degrees differently?

Solution

I didn’t have much luck with strategy 1, so let’s consider strategy 2. How can we handle nodes with large degrees differently to allow for efficient processing? One approach is to have high-degree nodes record their updates and have nodes that need to know their previous color poll from these high-degree nodes. However, if there are $V$ nodes with high degrees, this approach seemingly does not provide much improvement.

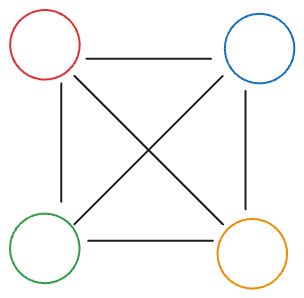
Graph of All Nodes with High Degree

An important observation stems from the handshake lemma, which states that the sum of the degrees equals twice the number of edges in the graph. Notice given the number of edges $E$, there can only be $2\sqrt{E}$ nodes with degree $\geq \sqrt{E}$.

Note that if there are $> 2\sqrt{E}$ nodes with degree $\geq \sqrt{E}$, then $\sum_{v} deg(v) > 2\sqrt{E} \times \sqrt{E} = 2E$, which contradicts the fact that we only have $E$ edges.

This gives us an upper bound of $O(\sqrt{E})$ vertices with high degrees. Since $E \leq 200000$, We can answer all queries with $O(Q\sqrt{E})$ time complexity.

An operation on any node requires polling of at most $O(\sqrt{E})$ heavy nodes. An update for a light node also loops through at most $O(\sqrt{E})$ neighbours.

With that, we have our solution sketch. We split the nodes into light nodes and heavy nodes, where those with degree $\geq \sqrt{E}$ degree are considered heavy nodes, and those with less are considered light nodes. We keep track of each node’s color and the time when the color was applied (e.g. $k$ if it is applied as the $k$-th operation). For each operation, we find the newest color applied to the current node by polling all heavy nodes connected to it and comparing it with its current color (light nodes would have pushed the operation to the current node).

For each update, we record the new color for the current node. If the update is on a light node, we also loop through its neighbors and update their colors as well. Implementation details include tracking whether a node is colored because it was chosen for an operation or because it is a neighbor of a node that was chosen for an operation.

Implementation Details

Submitting my implementation of this gives a Wrong Answer (WA). What’s wrong?

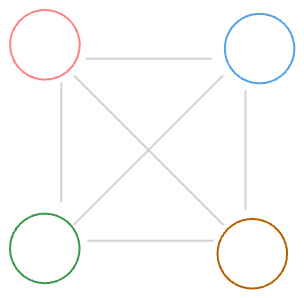
A subtle issue occurs when you only have one array keeping track of the current color of each node. You might miss some updates. Consider the following graph and operations:

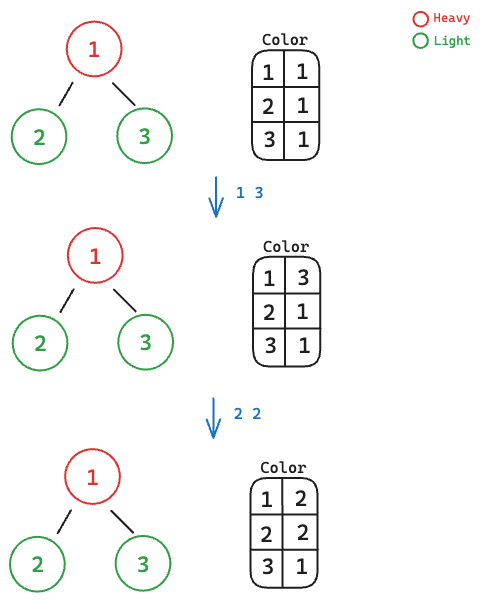
The 3rd node no longer knows it has been colored 3 before

Due to the 1st node being heavy, it does not apply the 1st operation to its neighbors. The 2nd node then colors itself and, since it’s a light node, it pushes the changes to the 1st node. Now, the 3rd node has no way of knowing it was colored by the first operation.

To circumvent this, keep track of two arrays: the first array keeps track of the color when a node is directly targeted by an operation (not colored by neighbors), and the second array keeps track of all changes, including when it is colored by neighbors.

When we poll from other heavy nodes, we only care about the color when the neighbor is itself chosen as the target of an operation. When we update, we should update both arrays for the chosen target of the operation, but only update the second array for its neighbors.

Code

#include <bits/stdc++.h>
using namespace std;

void fast_io() {
    ios_base::sync_with_stdio(0);
    cin.tie(NULL);
}

int V, E, Q;
vector<pair<int,int>> update_centre, update_by_others;
vector<int> deg;
vector<vector<int>> g;

int main() {
    fast_io(); cin >> V >> E;
    deg.assign(V,0); g.assign(V, {});
    update_centre.assign(V, {0,1}); update_by_others.assign(V, {0,1});

    for (int i = 0, u, v; i < E; i++) {
        cin >> u >> v; u--; v--;
        g[u].push_back(v);
        g[v].push_back(u);
        deg[u]++; deg[v]++;
    }
    const int SQRT_E = sqrt(E);
    for (int cur = 0; cur < V; cur++) sort(g[cur].begin(), g[cur].end(), 
        [&](const int u, const int v) { return deg[u] > deg[v];});

    cin >> Q;
    const auto node_is_heavy = [&](int node) { return deg[node] >= SQRT_E; };
    for (int q = 1, x , col; q <= Q; q++) {
        cin >> x >> col; x--;
        // get last color
        pair<int,int> cur_color = update_by_others[x];
        for (int child: g[x]) {
            if (!node_is_heavy(child)) break;
            cur_color = max(update_centre[child], cur_color);
        }

        cout << cur_color.second << '\n';

        update_centre[x] = update_by_others[x] = {q, col};
        if (node_is_heavy(x)) continue;
        for (int child: g[x]) update_by_others[child] = {q,col};
    }
}

Takeaway

Categorizing nodes based on their degrees, especially when the problem relates to their neighbors, is a valuable strategy. It’s also a good reminder to consider the handshake lemma, which hasn’t been used in a while.

Till next time!