Learner's Notes: Memory Order Side Chapter - The Story Of Strongly Happens Before
Strongly Happens Before?
It started innocently enough. I just wanted to brush up on C++ memory orderings. It’s been a while since I last stared into the abyss of std::atomic, so I figured, why not revisit some good ol’ std::memory_order mayhem?
Then I saw it. Strongly happens before.
Wait, what? When did we get a stronger version of happens before?
Turns out, it has been there for quite some time (since C++20 in fact), and it’s actually solving a very real problem in the memory model. If you’re also wondering what it is, why it exists, and whether you should care — that’s exactly what we’re going to explore today.
A simple program to start
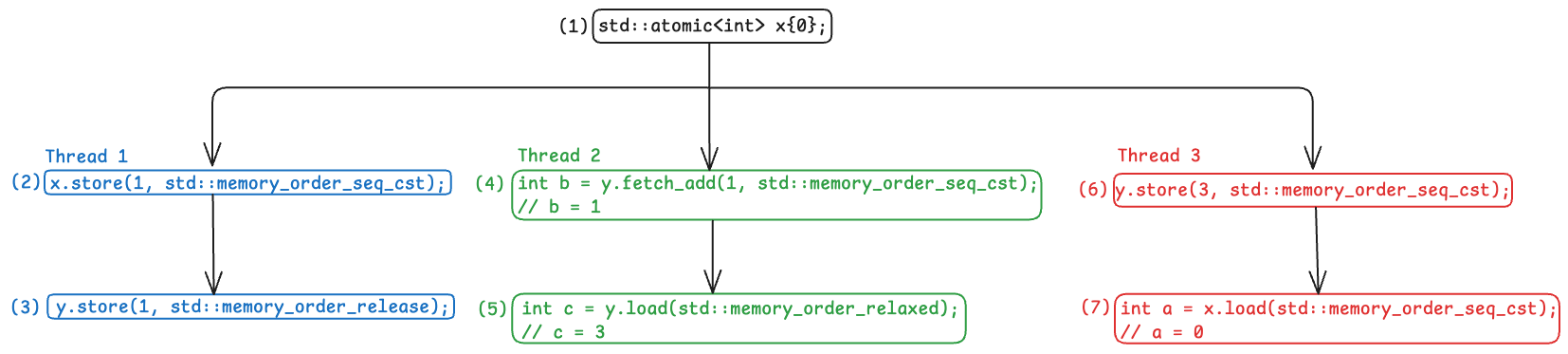
Let’s start off with a small program:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <atomic>
#include <thread>
std::atomic<int> x{0}, y{0};
void thread_1() {
// Thread 1
x.store(1, std::memory_order_seq_cst);
y.store(1, std::memory_order_release);
}
void thread_2() {
// Thread 2
int b = y.fetch_add(1, std::memory_order_seq_cst); // b = 1
int c = y.load(std::memory_order_relaxed); // c = 3
}
void thread_3() {
// Thread 3
y.store(3, std::memory_order_seq_cst);
int a = x.load(std::memory_order_seq_cst); // a = 0
}
int main() {
std::thread a(thread_1);
std::thread b(thread_2);
std::thread c(thread_3);
a.join(); b.join(); c.join();
}
The comments show the values each thread observed. Now, the big question: is this execution even possible under the C++ memory model?
Modification Order
Here’s where our little adventure begins. We’ll gradually build up the execution graph by adding edges as we layer in more constraints on the possible orderings.
Just to be clear, from [thread.thread.constr]/6:
The completion of the invocation of the constructor synchronizes with the beginning of the invocation of the copy of f.
This gives us a synchronizes-with relationship between thread construction and the start of the thread function. As a result, we’re allowed to establish the initial happens-before edges in the graph.
The first set of constraints we’ll add are all related to the modification order of x and y. As a quick refresher (from [intro.races]/4):
All modifications to a particular atomic object M occur in some particular total order, called the modification order of M.
Note that this total order exists per atomic object. Let’s bring in a few more rules from [intro.races] to get a clearer picture of the constraints imposed through modification order. Here are the relevant sections:
An evaluation A happens before an evaluation B (or, equivalently, B happens after A) if either
- A is sequenced before B, or
- A synchronizes with B, or
- A happens before X and X happens before B.
If an operation A that modifies an atomic object M happens before an operation B that modifies M, then A is earlier than B in the modification order of M. (write-write coherence)
If a value computation A of an atomic object M happens before a value computation B of M, and A takes its value from a side effect X on M, then the value computed by B is either the value stored by X or the value stored by a side effect Y on M, where Y follows X in the modification order of M. (read-read coherence)
If a value computation A of an atomic object M happens before an operation B that modifies M, then A takes its value from a side effect X on M, where X precedes B in the modification order of M. (read-write coherence)
If a side effect X on an atomic object M happens before a value computation B of M, then the evaluation B takes its value from X or from a side effect Y that follows X in the modification order of M. (write-read coherence)
Here’s an image to better illustrate the C++ coherence rules mentioned above. 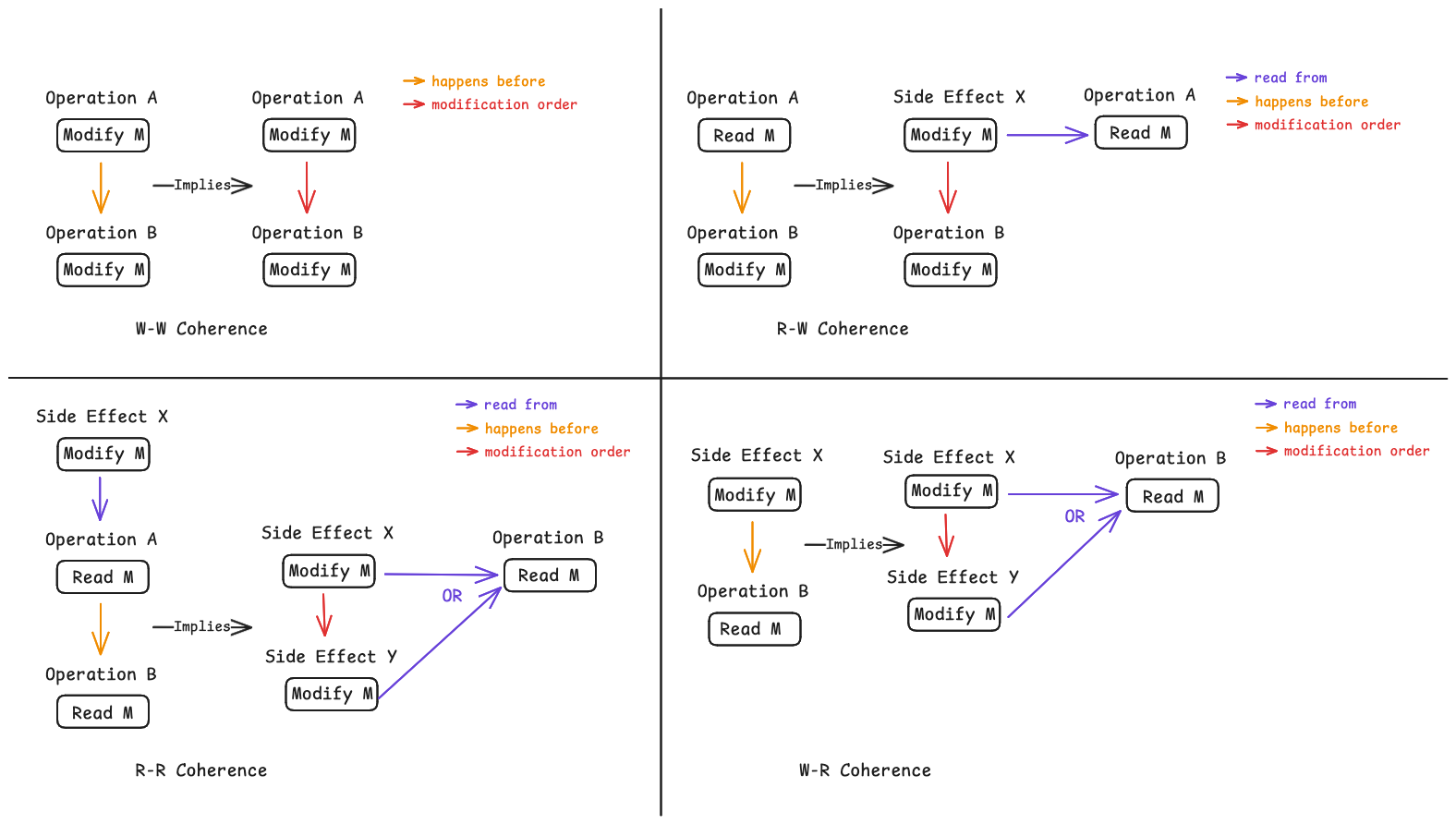
 Illustration for C++ Coherence Rules
Illustration for C++ Coherence Rules
Using these, we can now establish the following constraints in our execution:
- $(1) \rightarrow (2)$: Establish from write-write coherence, as $(1)$ happens before $(2)$.
- $(3) \rightarrow (4)$: Establish from write-write coherence, as $(3)$ happens before $(4)$ (synchronizes-with from [atomics.order]/2).
- $(4) \rightarrow (6)$: Establish from write-read coherence, as $(4)$ happens before $(5)$ hence $(5)$ can only takes its value from $(4)$ or some other side effect that follows $(4)$ in the modification order of
y. Since $(5)$ can only take the value of the write at $(6)$, $(6)$ must follow $(4)$ in the modification order ofy
Here is the current execution graph with the added constraints: 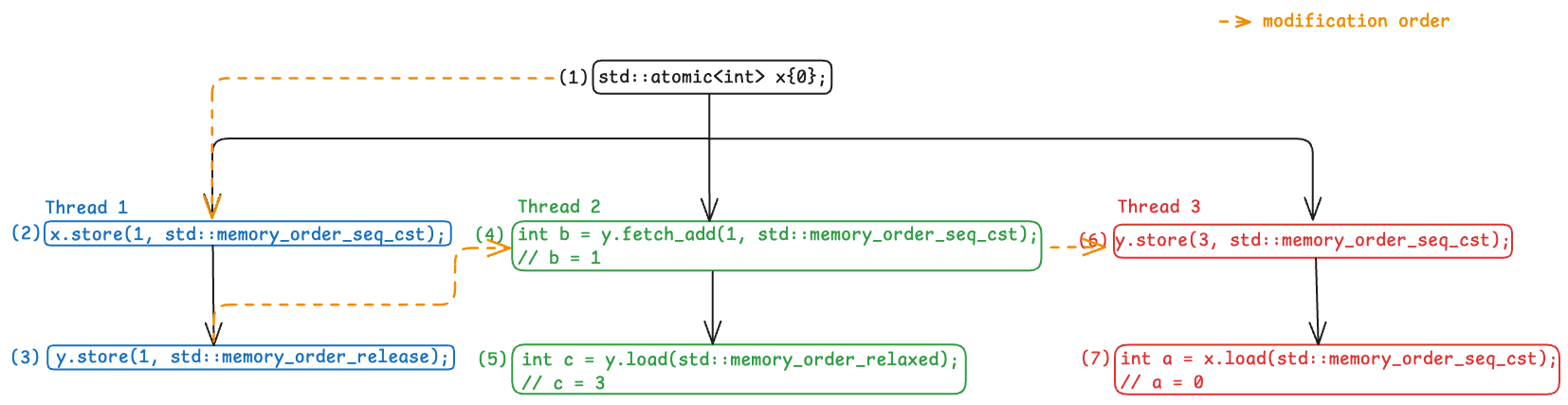
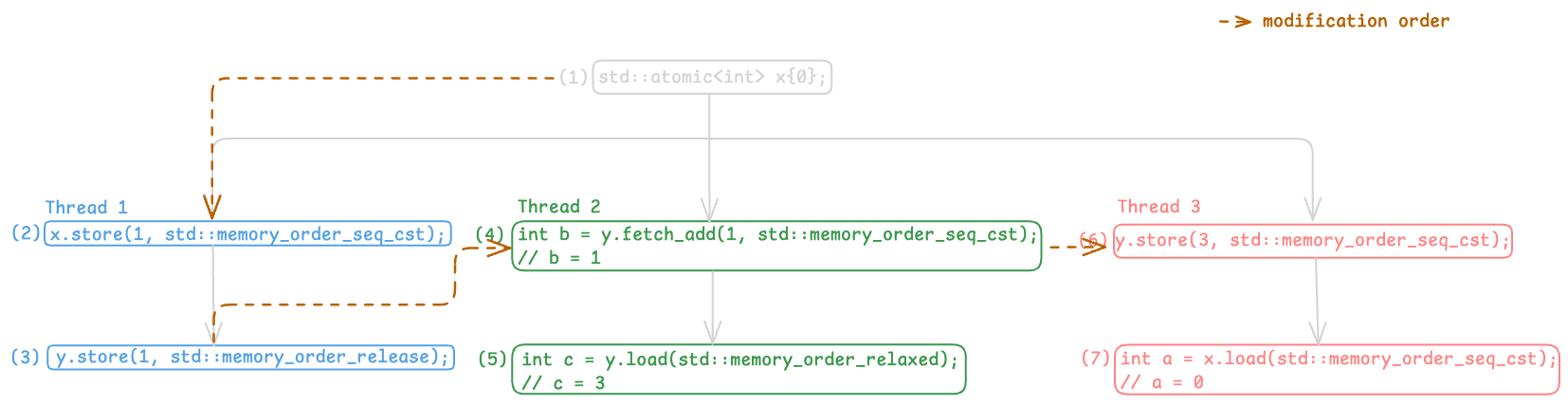 Execution Graph with Modification Order
Execution Graph with Modification Order
Coherence-Ordered Before
Let’s continue with another constraint, coherence-ordered before. To understand what this means, let’s take a quick look at [atomics.order]/3.
An atomic operation A on some atomic object M is coherence-ordered before another atomic operation B on M if
- A is a modification, and B reads the value stored by A, or
- A precedes B in the modification order of M, or
- A and B are not the same atomic read-modify-write operation, and there exists an atomic modification X of M such that A reads the value stored by X and X precedes B in the modification order of M, or
- there exists an atomic modification X of M such that A is coherence-ordered before X and X is coherence-ordered before B.
A few important things to note:
- The modification order we previously established is used to establish a coherence-ordered before relationship.
- The coherence-ordered before relation is transitive.
For our purposes, we’re mainly interested in the specific case described by the following criterion:
A is a modification, and B reads the value stored by A We’ll refer to this as the “read-from” relationship in the diagrams going forward, just to keep things visually clearer.
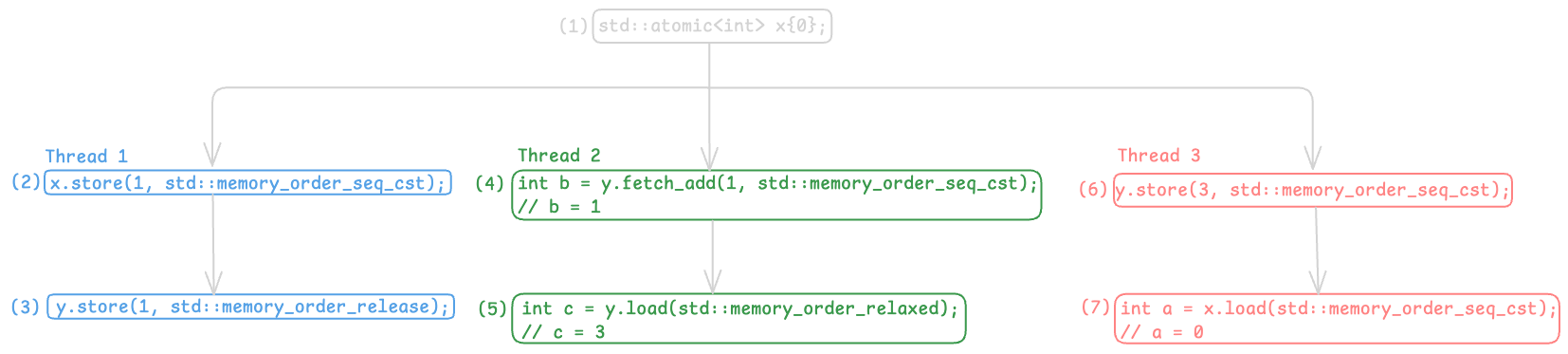
Here are the edges we can now add to our diagram, based on the read-from relationship:
- $(1) \rightarrow (7)$: $(7)$ reads from the value stored by $(1)$.
- $(3) \rightarrow (4)$: $(4)$ reads from the value stored by $(3)$.
- $(6) \rightarrow (5)$: $(5)$ reads from the value stored by $(6)$.
And with that, here’s the updated execution graph: 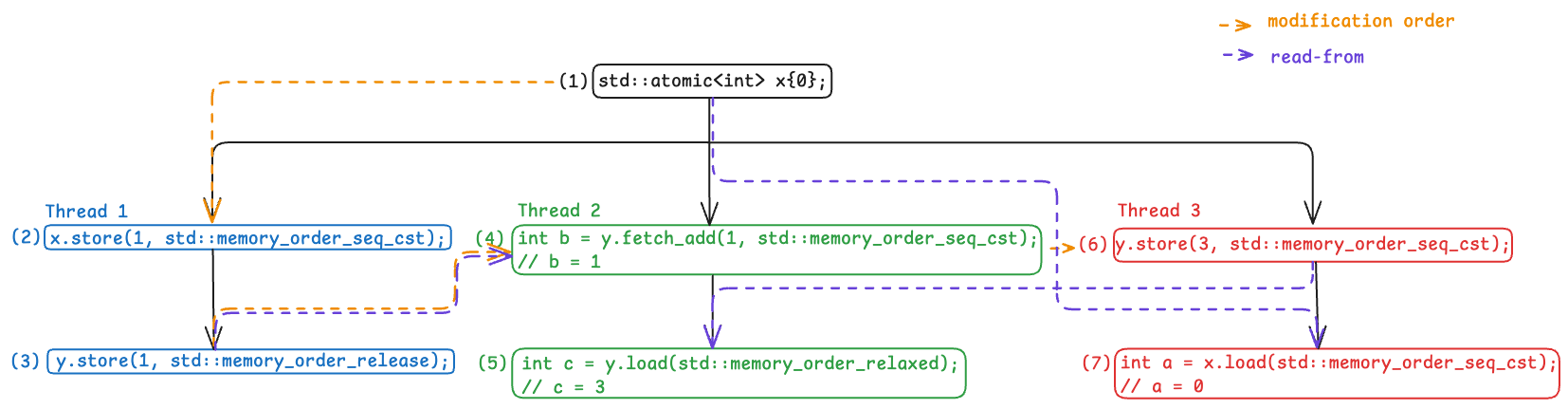
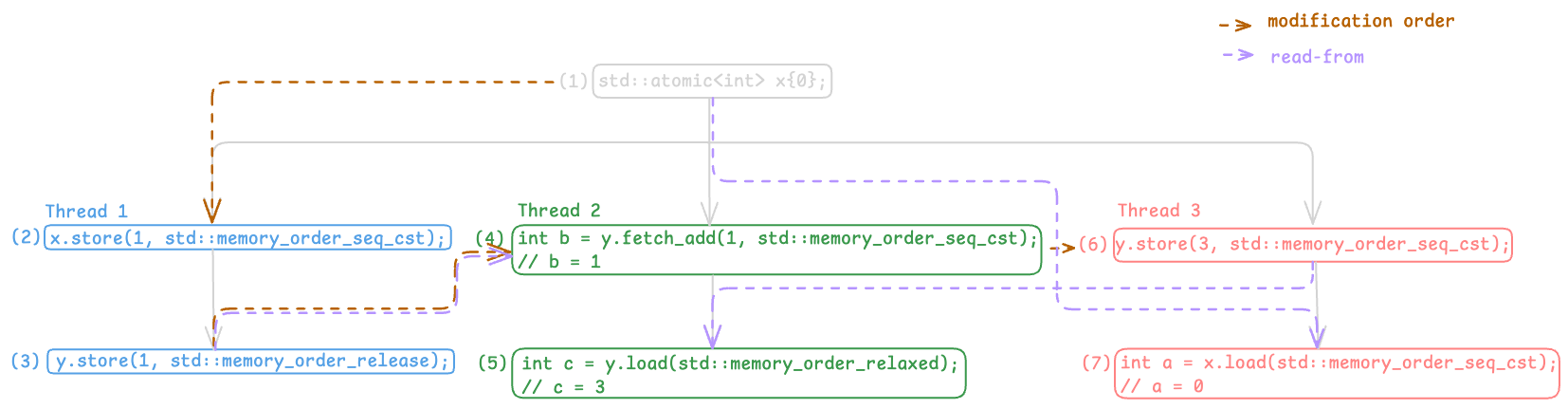 Execution Graph with Read-From Relationship
Execution Graph with Read-From Relationship
So far so good, we have a perfectly fine execution graph. However, let’s take a look if there’s anything we missed.
An atomic operation A on some atomic object M is coherence-ordered before another atomic operation B on M if
- …
- A and B are not the same atomic read-modify-write operation, and there exists an atomic modification X of M such that A reads the value stored by X and X precedes B in the modification order of M
- …
Interestingly, this gives us another constraint:
- $(7) \rightarrow (2)$: $(2)$ and $(7)$ are indeed not the same atomic read-modify-write operation, $(7)$ reads from $(1)$ and $(1)$ precedes $(2)$ in the modification order of
x.
We will use the “read-before” relationship to signify this in the execution graph, as shown here: 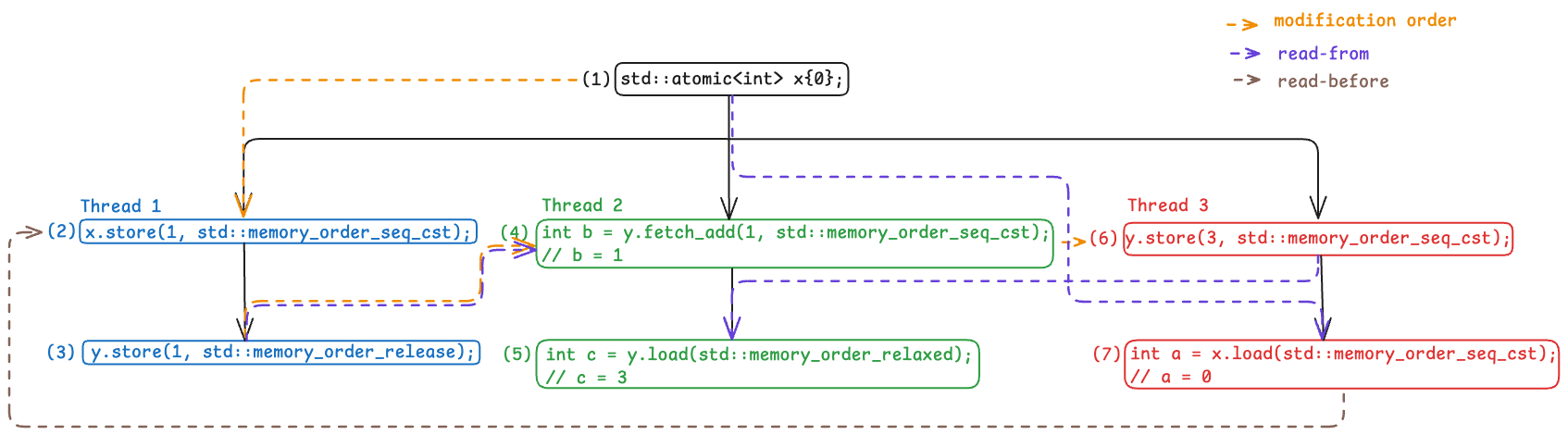
 Execution Graph with Read-Before Relationship
Execution Graph with Read-Before Relationship
Single total order
Alright, so what’s the point of going through all of this? The actual goal here is to establish a single total order over all memory_order::seq_cst operations. For that, let’s look at one final requirement from [atomics.order]/4:
There is a single total order S on all
memory_order::seq_cstoperations, including fences, that satisfies the following constraints. First, if A and B arememory_order::seq_cstoperations and A strongly happens before B, then A precedes B in S. Second, for every pair of atomic operations A and B on an object M, where A is coherence-ordered before B, the following four conditions are required to be satisfied by S:
- if A and B are both
memory_order::seq_cstoperations, then A precedes B in S; and- …
(We can safely ignore the rest for now, as we don’t deal with fences in this example.)
Now, this is where the strongly happens before relation comes into play. But for the sake of this blog, let’s momentarily relax the definition and replace “strongly happens before” with just “happens before” to see what happens.
Under this relaxed definition, we find that we cannot establish a total order over all memory_order::seq_cst operations due to a cycle in the graph: $(2) \rightarrow (4) \rightarrow (6) \rightarrow (7) \rightarrow (2)$. This cycle makes the execution inconsistent with the standard’s requirements for memory_order::seq_cst, rendering it not a valid execution.
So what’s the issue?
Reconciling Real-World Behavior with the C++ Standard
Unfortunately, this execution is allowed by certain compilers and architectures, notably Power. We’ll take a closer look at why that’s the case shortly. But for now, it’s important to highlight the key decision faced by the C++ committee:
Should the implementations be fixed, or should the C++ standard itself be adjusted?
According to P0668R5, enforcing a stricter rule would introduce a significant performance penalty on acquire/release synchronization, essentially defeating the purpose of memory_order_acquire and memory_order_release.
Given this tradeoff, the committee chose the alternative: fix the standard instead of the implementations.
Before we look at what that fix entails, it helps to understand why architectures like Power permit such executions in the first place.
Diving Into Power
The unfortunate reality is that the only real way to understand why this behavior is allowed is to look at the assembly generated, and that’s exactly what we’re going to do. You can find the full Godbolt link here to explore the generated assembly in more detail.
But first, let’s verify that the outcome is actually possible on the Power architecture using herd7. Here’s the test case we’ll use:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
PPC Strongly-Happens-B4-Example
{
x = 0;
y = 0;
0:r2=x; 0:r4=y;
1:r4=y;
2:r4=y; 2:r8=x;
}
P0 | P1 | P2 ;
li r1,1 | L_retry: | li r1,3 ;
stw r1,0(r2) | lwarx r1,r0,r4 | stw r1,0(r4) ;
lwsync | addi r2,r1,1 | sync ;
stw r1,0(r4) | stwcx. r2,r0,r4 | lwz r2,0(r8) ;
| bne L_retry | ;
| isync | ;
| lwz r3,0(r4) | ;
exists (1:r1=1 /\ 1:r3=3 /\ 2:r2=0)
And here’s the result from herd7:
1
2
3
4
Loop Ok
Witnesses
Positive: 1 Negative: 18
Condition exists (1:r1=1 /\ 1:r3=3 /\ 2:r2=0)
This confirms that the execution we previously marked as invalid under the “happens-before” interpretation is in fact valid on Power.
Below is the execution graph generated by herd7 for this scenario: 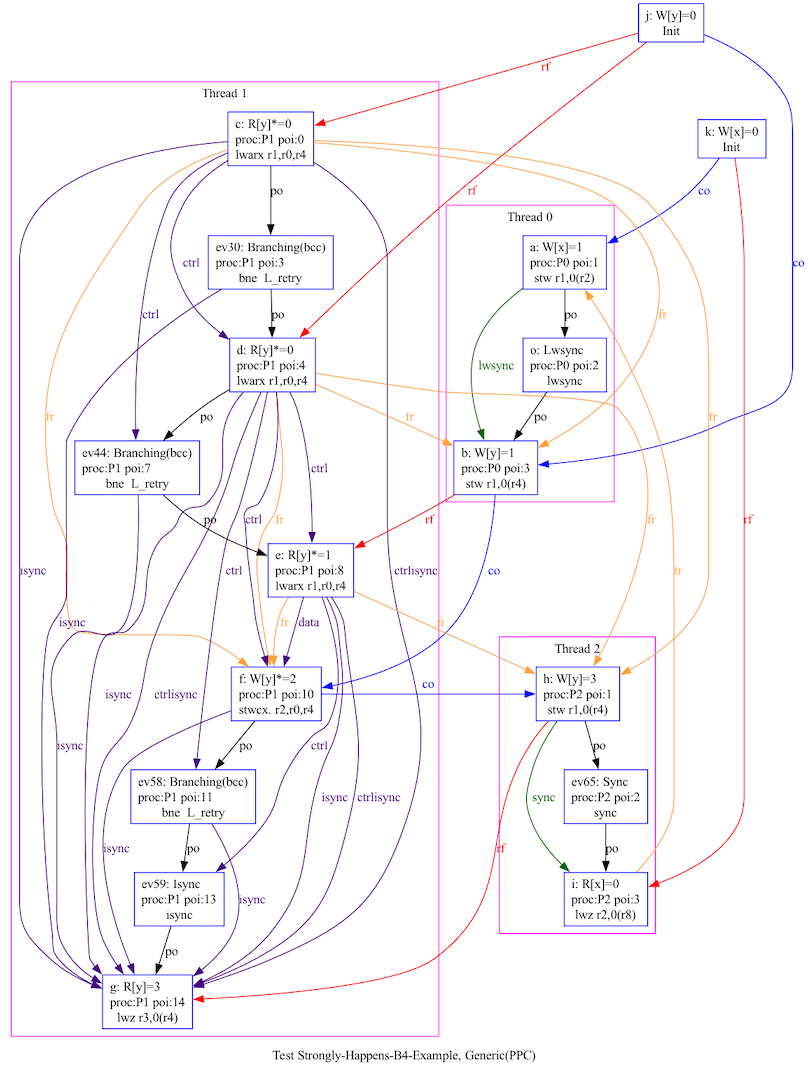
Now, we don’t need to understand every low-level detail, but we do need a rough sense of how synchronization works on Power. A good starting point is the PLDI 2011 paper on Understanding Power Multiprocessors along with this tutorial-style supplement. Additionally, it’s worth checking out the mapping of C++ atomic operations to instruction sequences, which sheds light on what instructions get emitted under various memory orders on different architectures.
However, for brevity, we’ll only highlight the relevant synchronization constructs and constraints here. First, let’s look at the memory barriers (taken from the tutorial notes):
| Operations | sync/hwsync | lwsync |
|---|---|---|
| $R \rightarrow R$ | For two reads separated by a sync, the barrier will ensure that they are satisfied in program order, and also will ensure that they are committed in program order | Same as sync/hwsync |
| $R \rightarrow W$ | For a read before a write, separated by a sync,the barrier will ensure that the read is satisfied (and also committed) before the write can be committed, and hence before the write can be propagated and thereby become visible to any other thread | Same as sync/hwsync |
| $W \rightarrow W$ | For a write before a write, separated by a sync,the barrier will ensure that the first write is committed and has propagated to all other threads before the second write is committed, and hence before the second write can propagate to any other thread | For a write before a write, separated by a lwsync,the barrier will ensure that for any particular other thread, the first write propagates to that thread before the second does. |
| $W \rightarrow R$ | For a write before a read, separated by a sync, thebarrier will ensure that the write is committed and has propagated to all other threads before the read is satisfied | For a write before a read, separated by a lwsync, the barrier will ensure that the write is committed before the read is satisfied, but lets the read be satisfied before the write has been propagated to any other thread |
Even though Power multiprocessors use a highly relaxed memory model, one key guarantee is preserved: For each memory location, there exists a single linear order of all writes to that location that must be respected by all threads. This property is known as coherence.
Here are a few important coherence constraints to help illustrate the idea:
- $R \rightarrow R$: A pair of reads by a thread cannot read contrary to the coherence order.
- $W \rightarrow W$: The coherence order must respect program order for a pair of writes by a thread .
- $W \rightarrow R$: A read cannot read from a write that is coherence-hidden by another write program-order preceding the read.
- $R \rightarrow W$: A write cannot coherence order-precede a write that a program-order-preceding read from.
For a clear illustration, see the coherence section in Understanding Power Multiprocessors.
Power Assembly Illustrated
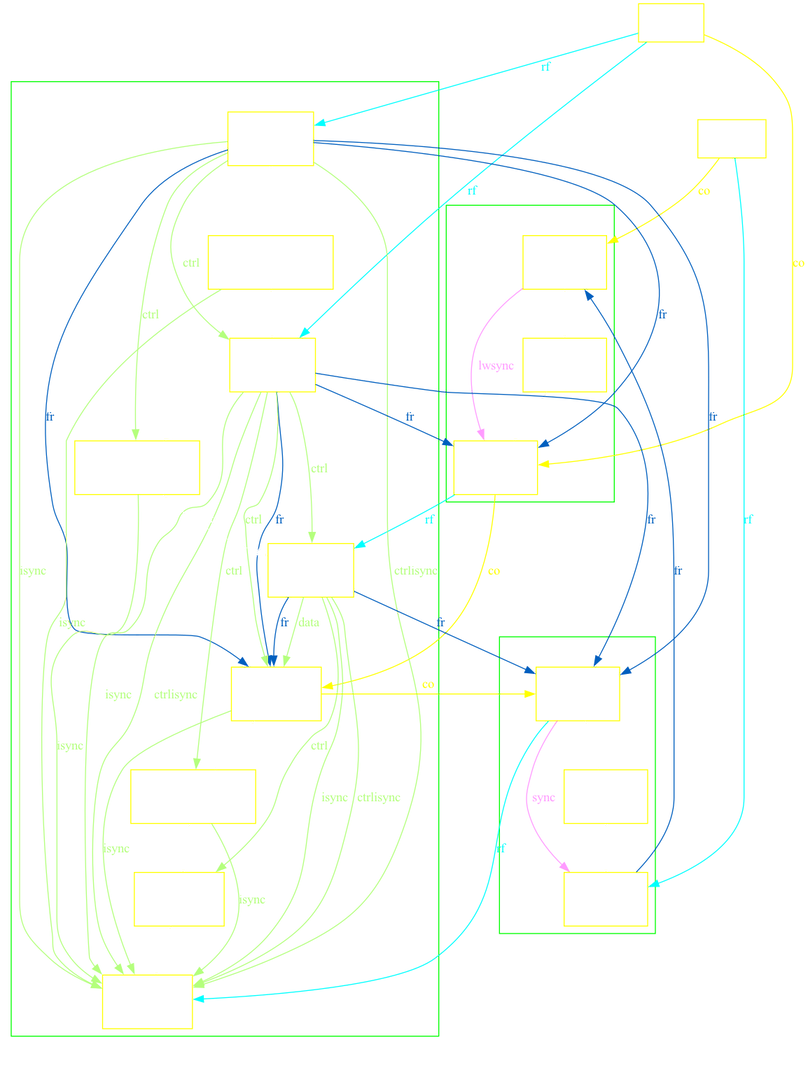
Now, let’s take a look at a simpler illustration of the program we’ve been examining: 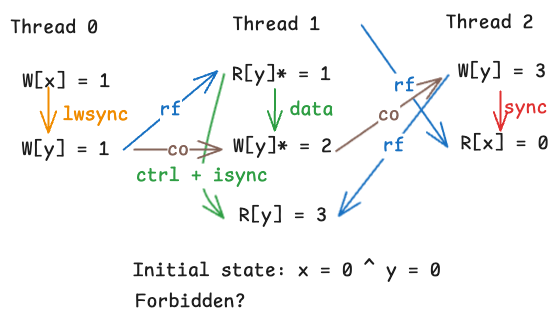
We want to understand why this execution is allowed on Power. Let’s walk through a few key observations:
- Thread 1’s $R[y]^* = 1$ implies that $W[y] = 1$ from Thread 0 must have propagated to Thread 1. By the $R \rightarrow W$ coherence rule, this means Thread 1’s $W[y]^* = 2$ must be coherence-ordered after $W[y] = 1$.
- Thread 2’s $W[y] = 3$ cannot be coherence-ordered before either $W[y] = 1$ or $W[y]* = 2$, because that would violate $W \rightarrow R$ coherence (as $R[y] = 3$ comes after).
- However, coherence does not require $W[y] = 1$ to propagate to Thread 2. And with only
lwsyncin Thread 0, $W[x] = 1$ is not required to propagate to Thread 2 either.
Hence, we have our following sequence of events:
- Thread 0 performs $W[x] = 1$ and $W[y] = 1$, and both writes propagate to Thread 1.
- Thread 1 reads $R[y]* = 1$, then writes $W[y]* = 2$.
- Thread 2 performs $W[y] = 3$ and issues a sync, forcing that write to propagate to Thread 0 and Thread 1 before the $R[x]$ is satisfied.
- Thread 1 reads $R[y] = 3$.
- Thread 2 reads $R[x] = 0$, since $W[x] = 1$ from Thread 0 never propagated to it.
Unfortunately, stwcx. appears to have issues when used with rmem. As an alternative, this example demonstrates the same behavior using regular stores and loads.
And there we have it, the trickiest part of this post! From here, we’re ready to transition back into the world of C++.
How Strongly Happens-Before Fixes the Example
Let’s explore what strongly happens-before actually means, as defined in [intro.races]/8.
An evaluation A strongly happens before an evaluation D if, either
- A is sequenced before D, or
- A synchronizes with D, and both A and D are sequentially consistent atomic operations, or
- there are evaluations B and C such that A is sequenced before B, B happens before C, and C is sequenced before D, or
- there is an evaluation B such that A strongly happens before B, and B strongly happens before D.
Now let’s revisit our example:

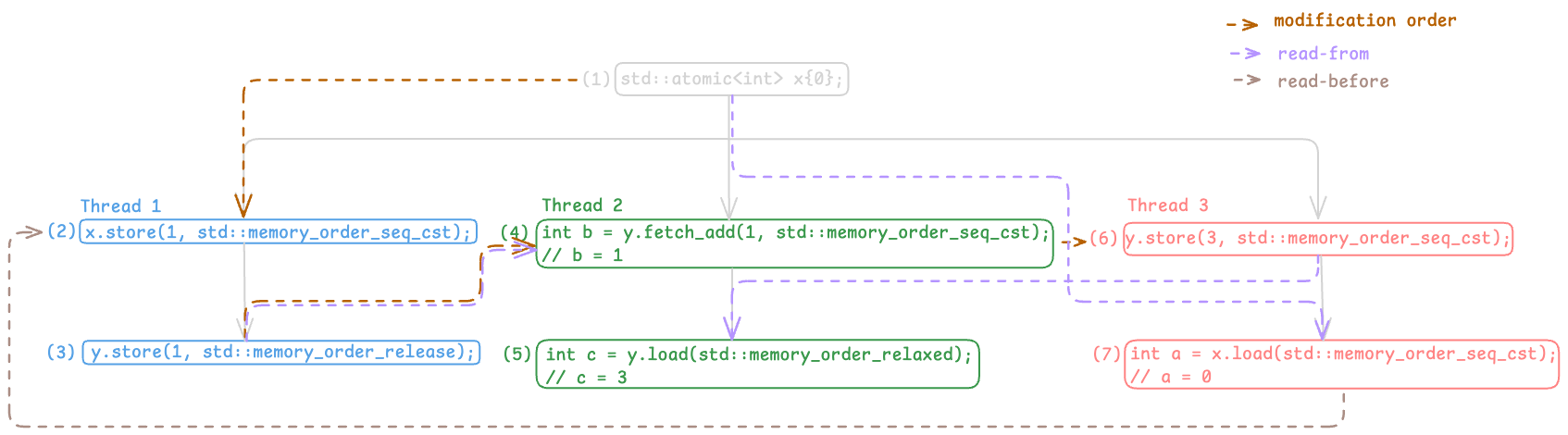
 Execution Graph with Read-Before Relationship
Execution Graph with Read-Before Relationship
Here, observe that the relation $(2) \rightarrow (4)$ does not satisfy any of the above conditions, so it does not qualify as a strongly happens-before relationship. As a result, in the single total order on all sequentially consistent operations, $(2) \rightarrow (4)$ is not necessarily preserved. In fact, to reflect the current observed behavior, we must not have $(2) \rightarrow (4)$. A valid total order consistent with this execution would be: $(4) \rightarrow (6) \rightarrow (7) \rightarrow (2)$.
Let’s take a look at the conditions that stands out here:
- A synchronizes with D, and both A and D are sequentially consistent atomic operations, or
- there are evaluations B and C such that A is sequenced before B, B happens before C, and C is sequenced before D
Recall from [atomics.order]/2:
An atomic operation A that performs a release operation on an atomic object M synchronizes with an atomic operation B that performs an acquire operation on M and takes its value from any side effect in the release sequence headed by A.
The first condition above is especially interesting as it’s not immediately obvious why both A and D must be sequentially consistent atomic operations. The crucial insight is that on the Power architecture, A and D will both have a sync/hwsync before them (for leading sync; trailing sync is shown in the diagram below).
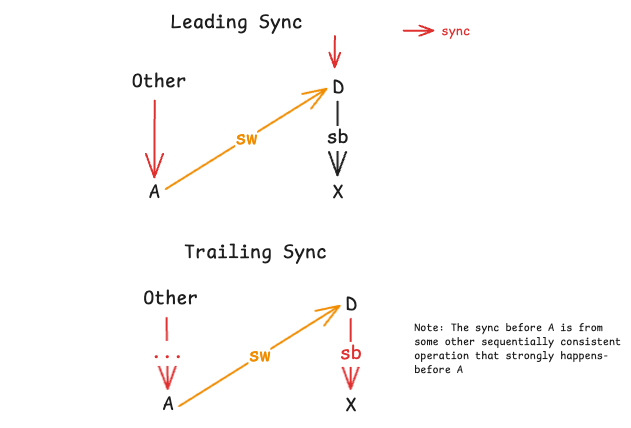
 Synchronizes With Example Where A and D Are Sequentially Consistent
Synchronizes With Example Where A and D Are Sequentially Consistent
Note that D, and any sequentially consistent atomic operations that strongly happen after D, must observe the effects of those that strongly happen before A, precisely due to the placement of sync/hwsync.
The second condition is equally fascinating. It ensures that a sync/hwsync must exist somewhere along the path, thereby enforcing sequential consistency, even on Power.
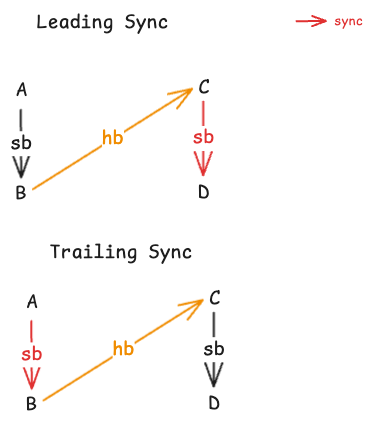
 Sequenced Before $\rightarrow$ Happens Before $\rightarrow$ Sequenced Before Example
Sequenced Before $\rightarrow$ Happens Before $\rightarrow$ Sequenced Before Example
One Last Question

 Execution Graph with Read-Before Relationship Let’s look at our example one more time. Earlier, we noted that the total order of sequentially consistent operations must not include $(2) \rightarrow (4)$. But at the same time, $(2)$ happens before $(4)$. Isn’t that a bit strange?
Execution Graph with Read-Before Relationship Let’s look at our example one more time. Earlier, we noted that the total order of sequentially consistent operations must not include $(2) \rightarrow (4)$. But at the same time, $(2)$ happens before $(4)$. Isn’t that a bit strange?
Indeed, this subtlety is even acknowledged in a note under [atomics.order]/6. This behavior only arises when mixing sequentially consistent and non-sequentially consistent operations on the same atomic object. As always, mixing memory orders is tricky, especially when subtle interactions like this come into play.
And that’s a wrap! If you managed to read till here, thank you! This took quite a bit of effort to write up as it is not easy to understand all the necessary prerequisites. Special thanks to Prof. Peter Sewell for pointing me to the tools available for verifying executions for Power.
Till next time!
Resources
- Repairing Sequential Consistency in C/C++11
- Proposal p0668r5
- C/C++11 mappings to processors
- Example POWER Implementation for C/C++ Memory Model
- Understanding POWER Multiprocessors
- A Tutorial Introduction to the ARM and POWER Relaxed Memory Models
- rmem Tool
- herd7 Tool
- Working Draft Programming Languages — C++